备用返回通道

题目描述：

牛客网有一个名为牛爱网神秘的入口。这天，牛可乐正在策划牛爱网的全新社交活动。每个人的账号在初始时都会被分配一个权重，第𝑖个账号的权重为𝑤𝑖。对于任意的两个账号𝑖和𝑗，如果它们的权重满足条件 (𝑤𝑖 & 𝑤𝑗) ≧ 1，即按位与运算结果大于或等于1，那么这两个账号会被分配到同一个社交网络中。

现有𝑛个账号，每个账号的权重已知，牛可乐希望知道，包含账号数量最多的社交网络中，包含多少个账号。

输入描述：

• 第一行输入一个整数𝑇，表示测试数据的组数。
• 对于每一组测试数据：
  • 第一行输入一个整数𝑛，表示账号的数量。
  • 第二行输入𝑛个整数𝑤1, 𝑤2, …, 𝑤𝑛，表示每个账号的权重。

输出描述：

• 对于每组测试数据，输出包含账号数量最多的社交网络中，包含的账号数量。

限制：

• 1 ≤ 𝑇 ≤ 10^5
• 1 ≤ 𝑛 ≤ 10^5
• 1 ≤ 𝑤𝑖 ≤ 10^18
• 单个测试文件的𝑛之和不超过10^5

示例输入：

2
5
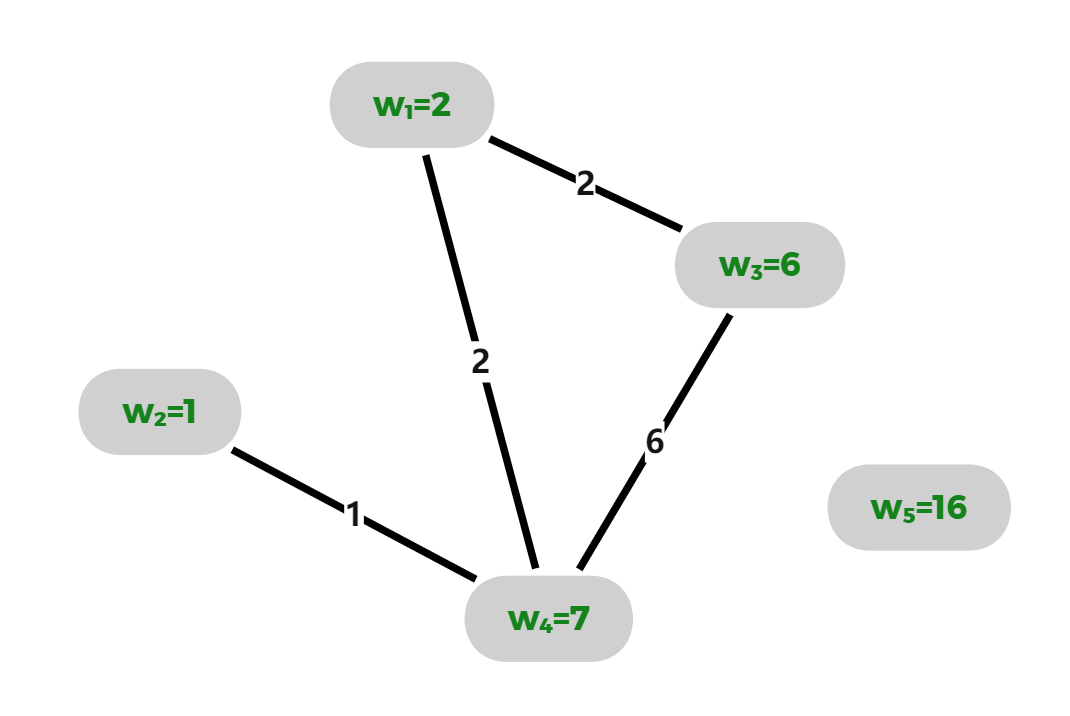
2 1 6 7 16
2
2 16

示例输出：

4
1

说明： 对于第一组测试数据，按位与运算的结果大于或等于1的账号形成社交网络，最大社交网络包含4个账号。 对于第二组测试数据，只有两个账号的按位与运算结果满足条件，因此最大的社交网络包含1个账号。

题解:

这个题目告诉我们题目的切入点以及思维方式的重要性. 比赛时间就那么长，我们应该选择尽可能优质的思维解题· 这里建议重点看优化思路，以留下第一印象

思路引导:

首先先看数据规模，以确定解决方法 我们可以看出,可以至少支持，我们的是算法应该是支持大约$O(n*log_2 n)$

常规思路(正向思维)

step1. 暴力枚举：
在暴力枚举中，你通过逐一检查所有可能的 二元关系 来构建社区。例如，对于每一对元素 <a, b>，你会检查它们是否连通，并根据这个检查结果来合并它们。直接地 ， 我们想通过枚举每个账号，来计算存在的二元关系S，那时间复杂度将会达到$O\left( \frac{1}{2} n^2 \cdot 60 \right)$ 显然行不通。

step2. 位运算的多元关系：
而使用位运算时，你实际上在 高效地利用位的表示特性 来优化这些二元关系S，从而生成 多元关系 E = S * S * …。 例如，你通过对比各个比特位的值来确定多个元素 是否属于同一社区，位运算将这个推导过程优化掉了。过程中用并查集维护就可以得到结果。时间复杂度大约是$O( n * 60*α(n))$，是能通过的。

优化思路(逆向思维)

• 我们一开始就面向着结果逆向推导:
  • 我们要找到这个 最大的社区 ：
    • 我们怎么样构造这个社区?
      • 整体的社区 又可能是由每 bit 位上的 子社区 合并来的。
      • 我们只需枚举 某个社区有谁 ，合并就可以。
    • 多个社区可能有重复怎么办?
      • 两个社区间有重复就意味着 联通，也就是要合并。如果用 并查集 会自动合并。
    • 我们在过程中记录所有社区集合的size的最大值就可以

代码实现